Mathematics of Tax-Advantaged Retirement Savings
(NOTE: The content of this blog is intended to demonstrate the mathematical analysis of retirement savings and is not intended as investment advice.)
How do you imagine most people pay expenses during their retirement, after they have stopped working and no longer receive a wage?
Almost everyone needs to save for retirement. There are a number of ways to do this. How can we make sense of the options we have and choose the best one? First, we need to provide some background and then we will get into the mathematics that can help us make these important decisions.
Background on Saving for Retirement
Saving for retirement is an important financial goal for most people.
- Social Security benefits are not likely to be enough to cover the expenses most people will face in retirement.
- Pensions that pay an annual amount for one’s entire retirement used to be common but are generally not provided by employers anymore.
To encourage retirement savings the government offers tax-based incentives for people to contribute to their retirement accounts.
Tax is an especially important consideration when saving for retirement. You potentially face two kinds of tax: first, a tax on your wages when they are paid and, second, a tax on the interest your investments earn.
Example: You invest $5000 for 20 years, earning an annual interest of 7%. How much would you have if there were no taxes?
- FV = 5000(1.07)20 = 19,300
Unfortunately, there is almost always tax! What how much would you have if a tax of 20% is applied to both the initial investment (your wages) and to the interest you earn each year?
- Your initial investment will now be reduced in value by 20%, 5000 • 0.8 = $4000
- After one year, your investment will have value 4000 • 1.07 = $4280 before taxes
- You now pay tax on the interest income – that’s the amount it increased by that year, not the entire amount, in this example your interest income in the first year will be 4280 – 4000 = $280. So you are taxed 20% of $280 which is $56 in taxes.
- After one year the final value of your investment will 4280 – 56 = $4224.
- If we work backwards, we can break down all our work, and rearrange the mathematics to see what’s going on:
4224
= 4280 – 56
= 4280 – (280 • 0.2)
= 4000 • 1.07 – 4000 • 0.07 • 0.2
= 4000 • (1.07 – 0.07 • 0.2)
= 4000 • (1 + 0.07(1 – 0.2))
= (5000 • 0.8) • (1 + 0.07(1 – 0.2))
- Notice that whatever the initial amount c invested, after one year, the value after tax will be c • (1 + 0.07(1 – 0.2)), in other words the tax makes you effectively earn interest at a lower rate, 0.07(1 – 0.2) = 0.056. So even though you are earning 7%, you are only really earning 5.6% after taking taxes into account.
- This means that after 20 years, the value of your investment will be worth FV = 4000 • 1.05620 = $11,900
Tax brings down the future value of your investment from $19,300 to $11,900 – a significant drop-off! In order to encourage retirement savings, the government provides some tax breaks which allow individuals to avoid paying some of these taxes provided they are saving that money to use in their retirement.
Tax-Incentive Based Retirement Accounts
There are two types of tax-incentive based retirement accounts we will discuss initially:
- Individual Retirement Account (IRA, often known as a “traditional IRA”)
- You pay no tax on your salary when it goes into the account.
- You pay no tax on income from interest earned in this account.
- You will pay tax when you withdraw from this account during retirement.
- The Roth IRA
- You will pay tax on your salary, even when it goes into the account.
- You pay no tax on income from interest earned in this account.
- You will pay no tax when you withdraw from this account during retirement.
Key facts to note:
- In all the tax-incentive based retirement accounts you pay no tax on income from interest.
- In all tax-incentive based retirement accounts withdrawals prior to retirement are taxed as income and also face an additional penalty for early withdrawal.
- In a traditional IRA, you pay no tax on your salary when it goes into the account but you pay tax when you withdraw it at retirement.
- In a Roth IRA, you pay tax on your salary when it goes into the account but you pay no tax when you withdraw it at retirement.
See https://www.irs.gov/retirement-plans for more details and other types of retirement plans.
While we use the terms pre-tax and post-tax, others use the terms before-tax and after-tax to refer to the same concepts.
How Big of an Advantage Do Tax-Advantaged Retirement Accounts Provide?
We saw above that if there is a tax rate of 20% and return of 7%, the future value of a $5000 taxable investment is:
FV = (5000 • 0.8) (1 +0.07 • 0.8)20=$11,900
With a traditional IRA, there is no tax on the investment income and no tax at the time of your contribution, so prior to withdrawal, the value is 5000(1.07)20 = 19,300, but you are taxed at 20% when you withdraw the money at retirement, so the amount you have to spend in retirement after taxes is:
FV = 5000(1.07)20 • 0.8 = $15,500
How much more do you have with a traditional IRA than a taxable investment? We can find how much more, as a percent, by taking the ratio of the two values:
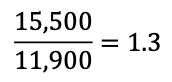
In other words, in the above example, your investment is worth approximately 30% more with a traditional IRA than a taxable investment.
We can also arrive at this number using the original algebraic expressions and simplifying:

Again, arriving at the same ratio, showing that in this example your investment would be worth approximately 30% more with a traditional IRA than a taxable investment.
However, this is just one example. Using a similar approach we can explore these same ideas to generalize…
Would you like to see the rest of this lesson in a student-friendly format? To keep reading