What are the Odds?

With the growth of online betting, odds are in the media more than ever. While we don’t recommend gambling, for reasons you will soon learn, we believe that understanding odds will improve your understanding of probability and investing.

Odds and probability

In math class, when we study uncertain outcomes we usually talk about probability, but in the popular media, especially when talking about who will win a sports event, they typically talk about “the odds.” Since they both relate to uncertain outcomes there should be a relationship between the two of them. While odds are frequently used in sports, they are also used in other areas. For example, credit scores are based on the odds of the borrower failing to make a payment vs making a payment on a financial obligation.

Studying odds can help improve your understanding of probability and investing. In fact, the earliest known mathematical treatment of probability, by the very famous and talented mathematicians Pascal and Fermat in 1654, was in the context of a problem from gambling.

Odds can be defined as a ratio of the expected or implied frequency of something happening to the expected or implied frequency of that event not happening. If someone says the odds are 3 to 1 that the train will be late today. They mean that it is three times as likely to be late than not be late. Probability on the other hand is the chance of something happening as a percentage of all possible outcomes. Using the above example, there would be a 75% probability of the train being late today.

Often expressed as percentages, probabilities are always between 0 and 1. With 0 meaning it never happens and 1 meaning it always happens. Odds can be any number but are often quoted as one whole number to another whole number. Odds could be quoted as 5 to 4 or 7 to 3.

Ratios and percentages

Suppose your team’s record against the cross-town rival so far this season is three wins and two losses.

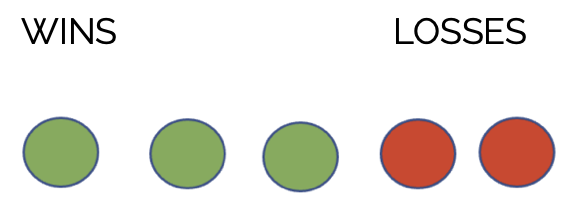
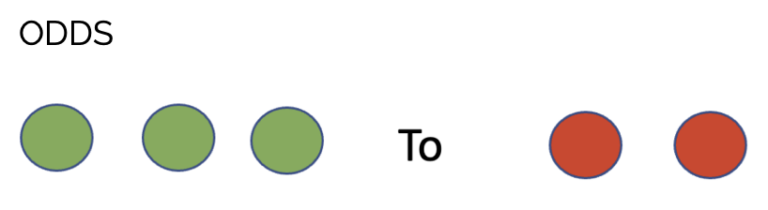
If that record is representative of the overall skill of the two teams, then the odds of your team winning the next game is 3 to 2 (or sometimes 3:2). This is the same as if you were asked “What is the ratio of wins to losses?” The answer would be: “3 wins to 2 losses.” Odds are the ratio of the event happening to the event not happening.

What if you were asked, “What is the probability of your team winning?” In this case, you would say “My team won 3 out of 5 games,” or “60% of the time.” If that percentage holds, then there is a 60% chance of my team winning the next game. Notice that probabilities are like percentages in that they represent the percentage of times that the event occurred divided by the total number of events. In this case, the total number of wins is divided by the total number of games played between those two teams. Probabilities are often expressed as a percentage but also can be expressed as fractions.